The idea is to write an article, related not so to Diplomacy, but to a given supply center, in my case the supply center of Vienna.
CDFv 2021 – Interview de Cyrille Sevin
Vainqueur de la première édition du CDFv (Championnat du monde francophone virtuel)
The event itself was designed to be as close as possible to the vWDC organized by Bill Hackenbracht (with Markus Zijlstra as non-player TD) as this event proved to be a complete success. As I have a (very!) long face-to-face player history (whereas I nearly never played online) it proved to be really an excellent substitute, and not only for this pandemic era.
As often in Europe, the system used was the C-Diplo 7 years of play, and the tournament winner would be the player with the most centers on the Top Board. There is a huge bonus for topping the board in C-Diplo. We had less players than expected sadly, only good thing then was it was easier to qualify.
The draw gave me Austria, always very challenging with a game very often decided in the first year. Italy was Ruben Sanchez, with whom my history was troubled. Last 2 times we played together were in WDC final boards; both time he played all game against me. Even if it ended both times very bad for Ruben I didn’t feel comfortable, but my intention was anyway to play with him, as IA is usually my first choice. But very interesting for me was the Russian player, with whom I had played a strong RT the day before. As Maxim Popov in Germany and Luca Pazzaglia in France countered this magistrally, it turned out very badly for me as Russia, with 5 powers ganging against us 2. So I had to “prostitute” myself toward Turkey, organizing everything diplomatically in the West especially with England (advantage of having only 2 units left, you have time to negotiate 😉…) It paid off, Turkey topped largely the board whereas I managed to end with 3 centers for only 2 units the last 2 years… No less than CON, WAR and ROM!! Even if it was my worst game of the tournament, it gave me the final board…. And will be an excellent souvenir in my collection of “odd” games.
Anyway, my intention was to work with Italy. What made me change my mind was when Russia came to me and answered to my question concerning his relationship with Turkey with “well, he will let me the Black Sea”. I immediately saw the big opportunity for me. A DMZ in Gal was made possible (so I was safe regarding Italy) while giving also a strong appealing position for Russia, with UKR to take RUM and BLA and SEV to continue against Turkey. It was easy to convince Russia then and the plan worked extremely well. Italy needed to believe I would not stab so still helped against Turkey while I attacked him saying I would go against Germany (probably he saw it as his last chance so had to go for it). By end of 1902, Italy was down to 3 and Turkey to 2. I immediately saw that, with a need to contain France, the game was likely to go to one of us… I basically focused the rest of the game on reassuring my ally, arguing that a conflict between us would only favour France. He accepted a perpetual bounce in BUL while holding Army in Armenia every turn. As he was ahead, his chances were higher than mine (which I genuinely believe was true by then).
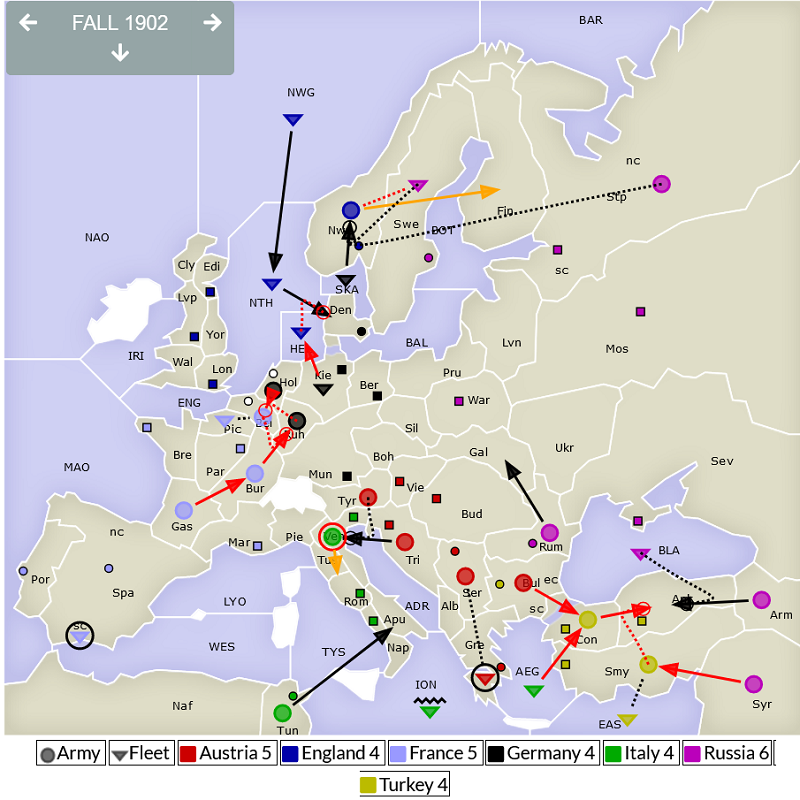
Last year was challenging. Having taken the whole Italy while Russia took the whole Scandinavia, I had MUN, he had BER and I was slightly ahead with 11-10. As the tiebreaker was not in my favour, I needed to keep this advance, even if MUN could not be kept. I was then lucky. First Russia was so afraid of me and probably under time pressure he lost NWY to England, just to send an Army Livonia which was unnecessary. Secondly, the tournament ranking system made that it was necessary for France to avoid a shared top (France would have then being 3rd of the tournament, against a 2nd place if no tie). So he supported me into BER after having taken MUN from me, ending the game in a 11-9-8 for me.
As often, the tournament was then won by a thin margin. On the 3 World DCs and 2 European DCs I won, only one win was clear. All others were decided only in the last year, which also make this game so exciting.

Possible positions
Introduction
Le problème à résoudre est le suivant : trouver le nombre de positions différentes à Diplomatie après le Printemps 1901.
Impossibilité d’une approche naïve
On devine aisément que le nombre en question est vertigineux. En effet, il y a sur la table exactement 22 unités (6 pays en possèdent 3 et 1 en possède 4). Si elles peuvent se rendre à 5 endroits (environ) chacune, on pourra atteindre l’ordre de grandeur de 522 = (arrondi par défaut) 2.38 x 10151 [1]. Il n’est donc pas question d’utiliser cette approche directe consistant à produire cette liste, la place occupée sur disque déborderait de celle de tout micro-ordinateur du commerce.
Pas question non plus d’énumérer les ordres possibles, appliquer un arbitre électronique, obtenir ainsi une position que l’on insère dans une liste dont on élimine soigneusement les doublons. Un arbitre électronique tout à fait honnête réalisant 1000 arbitrages à la seconde consommerait un temps tel qu’il faudrait passer la consigne aux générations futures de recueillir le résultat.
Etape 1 : par pays
Comme tout problème combinatoire, il faut le décomposer, on va donc commencer par lister les positions de départ par pays. On peut déjà constater que tout jeu d’ordre peut être écrit de manière « canonique ». Que signifie cela ? Que l’on peut classer les ordres en deux catégories :
- Les ordres de mouvements couronnés de succès à l’issue de la résolution,
- Les autres.
Si on change tous ces derniers (les ordres qui n’ont pas été arbitrés par un mouvement) par un ordre de tenir sur place, et si on laisse les autres, on obtient alors exactement le même résultat.
Quelles sont les possibilités pour une unité donnée ? Rester sur place, se rendre sur une zone accessible. On parlera de zone pour distinguer les trois zones suivantes : stpcs, stpcn, stp. Ces trois zones restent rattachées à une seule région, stp. Dans la grande majorité des cas, la région attachée garde le même nom que la zone.
On récupère une liste de voisinages par flotte et une liste de voisinages par armée (tout programme d’arbitrage de Diplomatie en possède nécessairement une)
Voici un extrait du fichier déclarant les voisinages :
| (ARMEEVOISIN MON GRE) |
| (ARMEEVOISIN MON SER) |
| (ARMEEVOISIN MON TRI) |
| (ARMEEVOISIN ANK CAU) |
| (ARMEEVOISIN ANK CON) |
| (ARMEEVOISIN ANK SMY) |
| (ARMEEVOISIN APU NAP) |
On utilise ces voisinages pour obtenir, pour chaque unité, toutes ses nouvelles positions possibles (sous forme de zone), et donc, pour un triplet (quadruplé) d’unités, en combinant toutes les positions des unités du pays sous forme « brute ». Bien entendu, une flotte utilise les « FLOTTEVOISIN » et une armée les « ARMEEVOISIN ».
Il faut cependant purger cette liste en ne conservant que les cas où les trois (quatre) unités occupent des régions distinctes, ce qui est assez facile. Notre distinction entre zone et région est là opportune, car elle permet de refuser le résultat de {f stpcs t, a mos – stp} qui conduit à deux unités sur la région stp.
Un autre cas de figure est moins immédiat, mais doit aussi être purgé de la liste. On définit que des mouvements sont en opposition s’ils sont effectués par deux unités (voisines) dont chacune cherche à prendre la place de l’autre, ou plus précisément à venir dans la région qu’occupe l’autre. Un exemple simple est {a rom – ven, a ven – rom}. Il faut donc encore écarter de notre liste les combinaisons comportant des mouvements en opposition.
Le résultat est-il alors le bon ? Non, car nous pouvons ainsi produire des doublons. Voici deux séquences d’ordres canoniques produisant des situations doublons, c’est à dire identiques : {a ven – rom, a rom – tos} et {a rom t, a ven – tos}. Il n’est en effet pas inscrit sur les unités le nom de leur emplacement d’origine.
Cette dernière purge nous permettra d’obtenir un résultat correct, confirmé par d’autres sources du zine VOPALIEC2 [2].
Voici le nombre de déploiements possibles par pays :
| Russie | 425 |
| Allemagne | 160 |
| Italie | 98 |
| Autriche | 97 |
| France | 93 |
| Angleterre | 88 |
| Turquie | 40 |
On remarque au passage que ces données confirment une vague opinion admise que la Turquie est un pays simple, et l’Allemagne un pays compliqué. La Russie, forte de ses 4 unités, peut donc se déployer de plus de manières, mais son cas n’est pas comparable.
Etape 2: par groupe de pays
Fort de notre liste de déploiements par pays, reste à poursuivre en cherchant à regrouper plusieurs pays. Dans l’absolu, si ces 7 pays n’interagissaient pas, la solution serait simplement le produit de ces 7 valeurs, à savoir environ 425 x 160 x 98 x 97 x 93 x 88 x 40 = (arrondi par défaut) 2.11 x 1014. Bien entendu certaines incompatibilités sont évidentes, entre deux pays suffisamment voisins, comme l’Angleterre et la France, le déploiement {man, edi, yor} de cette première ne peut cohabiter avec le déploiement {man, par, tou} de cette dernière.
On pourrait (et on l’a fait) calculer le nombre d’incompatibilités pour chacun des (7 x 6) / 2 = 21 paires de pays, multiplier chaque résultat par le produit des déploiements possibles pour les 5 autres pays. En retranchant ensuite la somme de toutes ces incompatibilités du produit de tous les déploiements possibles, on obtiendrait un résultat assez voisin de la solution, mais tout de même erroné, parce que l’on aurait retranché au moins deux fois (donc une de trop) un 7-uplet de déploiements présentant des incompatibilités sur deux paires de pays d’intersections non vides. On appellera par la suite cette méthode la « mauvaise méthode ».
Après avoir bien observé la carte de Diplomatie, on va regrouper nos pays de la manière suivante :
Pour calculer le nombre de déploiements possibles pour deux pays, on produit tous les couples possibles, puis on réalise les mêmes purges que si toutes les unités étaient du même pays, dont on fera l’économie d’une répétition. La purge écartant le cas où des unités de même type ont interverti leurs positions n’est cependant pas à réaliser, en effet, d’une part elles ne sont pas de même nationalité donc distinctes, d’autre part cet état de fait est impossible (seules les armées de ven et tri pourraient être échangées, ce qui est impossible car cela nécessiterait des mouvements en opposition).
On trouve ainsi
- 7700 déploiements pour Angleterre et France ;
- 7138 déploiements pour Italie et Autriche ;
- 13 271 déploiements pour Russie et Turquie.
Reste à composer {Italie, Autriche} avec Allemagne, opération délicate puisque le produit des possibles est de 7 138 x 160 = 1 142 080. Purger ce million d’éléments est possible, mais il faut quelque peu optimiser le traitement, on économise donc déjà la vérification des conflits d’oppositions qui ne peuvent pas se produire entre des unités allemandes d’une part, italienne ou autrichiennes d’autre part.
Pour aller encore plus vite (car la lourdeur du calcul l’exige), on se limite à vérifier entre les éléments suivants :
- (Italie, 3ème unité) et (Allemagne, 3ème unité)
- (Autriche, 2ème unité) et (Allemagne, 3ème unité)
En effet, on a repéré les possibilités de conflits dans le tableau suivant :
| Pays | 1ère unité | 2ème unité | 3ème unité |
| Italie | nap | rom | ven => {alp} |
| Autriche | tri | Vie => {alp, boh} | bud |
| Allemagne | kie | Ber | Mun => {alp, boh, sil} |
De ces 1 142 080 éléments, seuls 1 023 641 restent après la purge.
On conserve donc soigneusement dans trois fichiers les déploiements possibles pour ces trois sous-ensembles de pays, et on va maintenant chercher le nombre de solutions de notre problème.
Etape 3 : partitionnement des sous-ensembles
Cette dernière étape sera un peu plus laborieuse. Rappelons d’abord la définition du partitionnement d’un ensemble : c’est lui trouver des sous-ensembles vérifiant les trois propriétés suivantes :
- Aucun n’est vide,
- Leur réunion est l’ensemble de départ,
- Ils sont disjoints deux à deux.
Etudions d’abord les déploiements de {Angleterre, France}. C’est en bou et pie qu’ils interfèrent avec le reste de l’Europe et de manière indépendante.
Notre partition aura donc 4 éléments :
| Repère | bou | pie | Nombre |
| A1 | Oui | Oui | 418 |
| A2 | Oui | Non | 2244 |
| A3 | Non | Oui | 1408 |
| A3 | Non | Non | 3630 |
Etudions ensuite les déploiements de {Russie, Turquie}. C’est en gal, pru et sil qu’ils interfèrent avec le reste de l’Europe, et de manière dépendante cette fois. C’est l’unité en var au départ qui cause ce conflit, les occupations sont donc incompatibles deux à deux.
Notre partition aura donc 4 éléments :
| Repère | Repère | Nombre |
| B1 | Gal | 2634 |
| B2 | Pru | 2634 |
| B3 | Sil | 2634 |
| B4 | ∅ | 5369 |
Etudions enfin les déploiements de {Allemagne, Autriche, Italie}. C’est en pie, bou, gal, pru et sil qu’ils interfèrent avec le reste de l’Europe, et de manière presque indépendante. Nous expliquerons ce « presque » ultérieurement
Notre partition aura donc 32 éléments :
| Repère | pie | sil | pru | Nombre | ||
| C1 | Oui | Oui | Oui | Oui | Oui | 80 |
| C2 | Oui | Oui | Oui | Oui | Non | 3192 |
| C3 | Oui | Oui | Oui | Non | Oui | 3192 |
| C4 | Oui | Oui | Oui | Non | Non | 7980 |
| C5 | Oui | Oui | Non | Oui | Oui | 0 |
| C6 | Oui | Oui | Non | Oui | Non | 8250 |
| C7 | Oui | Oui | Non | Non | Oui | 8250 |
| C8 | Oui | Oui | Non | Non | Non | 20625 |
| C9 | Oui | Non | Oui | Oui | Oui | 3192 |
| C10 | Oui | Non | Oui | Oui | Non | 17140 |
| C11 | Oui | Non | Oui | Non | Oui | 17140 |
| C12 | Oui | Non | Oui | Non | Non | 29550 |
| C13 | Oui | Non | Non | Oui | Oui | 8250 |
| C14 | Oui | Non | Non | Oui | Non | 42262 |
| C15 | Oui | Non | Non | Non | Oui | 42262 |
| C16 | Oui | Non | Non | Non | Non | 71280 |
| C17 | Non | Oui | Oui | Oui | Oui | 0 |
| C18 | Non | Oui | Oui | Oui | Non | 9228 |
| C19 | Non | Oui | Oui | Non | Oui | 9228 |
| C20 | Non | Oui | Oui | Non | Non | 23070 |
| C21 | Non | Oui | Non | Oui | Oui | 0 |
| C22 | Non | Oui | Non | Oui | Non | 22158 |
| C23 | Non | Oui | Non | Non | Oui | 22158 |
| C24 | Non | Oui | Non | Non | Non | 55395 |
| C25 | Non | Non | Oui | Oui | Oui | 9228 |
| C26 | Non | Non | Oui | Oui | Non | 47108 |
| C27 | Non | Non | Oui | Non | Oui | 47108 |
| C28 | Non | Non | Oui | Non | Non | 79320 |
| C29 | Non | Non | Non | Oui | Oui | 22158 |
| C30 | Non | Non | Non | Oui | Non | 108276 |
| C31 | Non | Non | Non | Non | Oui | 108276 |
| C32 | Non | Non | Non | Non | Non | 178365 |
Des cas impossibles (nombre = 0) sont restés dans notre partitionnement. Le premier rencontré, par exemple, correspond à une unité en pie, bou, sil et pru, et pas d’unité en gal. C’est ber et mun qui peuvent occuper pru, sil et bou, et occuper les trois à la fois pour ces deux unités est impossible. La présence de ces cas impossibles résulte du petit manque d’indépendance des combinaisons. Nous pouvons les laisser car ils ne gênent pas la suite des calculs, bien qu’un « bon » partitionnement ne tolère pas d’ensembles vides.
On en profite pour vérifier au passage que la somme des nombres d’éléments pour chaque partitionnement fournit bien le nombre d’éléments total de l’ensemble partitionné.
Etape 4 : décompte exhaustif
Il faut maintenant combiner toutes ces possibilités. On peut se trouver dans 4 x 4 x 32 = 512 cas différents, certains sont plausibles (s’il n’y a aucun conflit), les autres ne le sont pas. Pour chaque triplet différent, le produit des trois nombres donne une valeur, et ce sont ces valeurs qu’il faut ajouter pour obtenir notre résultat.
Voici un exemple de combinaison possible et un exemple de combinaison impossible :
- {A4, B6, C32} est possible, aucun conflit.
- {A2, B3, C8} est impossible, car il y a un conflit sur bou.
On liste donc les 512 cas de figure différents, et on ne sélectionne que ceux pour lesquels il n’y a pas conflit.
Concrètement, l’absence de conflit signifie que :
- bou n’est pas occupé à la fois dans {France, Angleterre} et {Allemagne, Italie, Autriche}.
- pie n’est pas occupé à la fois dans {France, Angleterre} et {Allemagne, Italie, Autriche}.
- Si var est allée en gal dans{Russie, Turquie}, gal n’est pas occupé dans {Allemagne, Italie, Autriche}
- Si var est allée en sil dans{Russie, Turquie}, sil n’est pas occupé dans {Allemagne, Italie, Autriche}
- Si var est allée en pru dans{Russie, Turquie}, pru n’est pas occupé dans {Allemagne, Italie, Autriche}
On obtient donc une liste de 180 triplets, il faut donc réaliser les 180 produits, puis la somme des 180 résultats.
Le résultat obtenu est donc : 74 980 036 938 664.
(Ou, en français, environ soixante-quinze mille milliards, en notation scientifique (arrondi par défaut) 7.49 x 1013)
Récapitulation et comparaison des estimations successives (arrondis par défaut) :
| Résultat par la « Mauvaise méthode » |
Résultat |
Estimation à partir des déploiements par pays | Estimation grossière à partir des ordres |
| 7.47 x 1013 | 7.49 x 1013 | 2.11 x 1014 | 2.38 x 1015 |
Détails techniques
Les énumérations ont été réalisées grâce à plusieurs petits systèmes experts dont le moteur était une réalisation personnelle4 [4] de l’auteur (développée sous LINUX en Langage C). Ce moteur de système expert rustique avec variable utilise un sous-ensemble de la syntaxe OPS5. Il permet d’écrire typiquement des règles de la forme5 [5] :
Exemple d’inférence :
|
Base de règles |
Base de faits initiale |
Fait résultant de l’inférence |
|
Si (pere ?x ?y) (pere ?y ?z) alors (grand_pere ?x ?z) |
(pere Jeremie Michel) (pere Michel Paul) } |
(grand_pere Jeremie Paul) |
L’algorithme RETE6 [6] y est implémenté de manière standard, il permet d’optimiser fortement les calculs aux prix d’une très forte occupation de la mémoire. L’utilisation du prédicat « DIFF » a servi par exemple à détecter les triplets de zones d’arrivé des unités d’un pays pour lesquels les 3 régions correspondantes sont bel et bien distinctes.
A chaque problème correspond une base de règle et une base de faits spécifique, l’inférence produisant les résultats escomptés. Programmer la résolution d’un problème avec un système expert est pratique, convivial et rapide.
Lorsque qu’il a fallu juste compter le nombre de chaque élément des partitions, ce sont les appels systèmes UNIX « grep » (recherche de chaîne de caractère dans un fichier, avec l’option « -v » pour une recherche inversée) et « wc » (compte du nombre de lignes, mots et caractères) qui ont été mis à contribution.
Voici un exemple de recherche dans l’ensemble des déploiements {Allemagne, Italie, Autriche} correspondant au cas C207 [7] :
cat italautall.txt | grep –v PIE | grep BOU | grep GAL | grep –v SIL | grep –v PRU | wc
Lorsqu’il a fallu réaliser 180 produits puis une somme de 180 termes, c’est EXCEL qui s’est chargé de l’opération, et encore de manière très conviviale. Un copier/coller dans un fichier texte sur PC du résultat de l’inférence, puis une importation de ce fichier texte dans un classeur EXCEL, une cellule (au sens EXCEL) de calcul de produit (dupliquée ensuite 179 fois), et une cellule réalisant la somme des 180 produits, et le tour est joué.
Conclusion
Le problème de trouver le nombre total de positions possibles en est un autre, plus mathématique, qui pourra faire l’objet d’une étude ultérieure. La méthodologie mise en place pourrait résoudre les casse-têtes liés aux positions de Diplomatie publiés de ci delà (reconstitution d’une partie à partir d’informations incomplètes.) Enfin les listes de positions possibles par pays produites pourraient aussi servir à revisiter la théorie des ouvertures.
Je serai ravi de toute confirmation de ce résultat par une autre personne pour le valider de manière définitive…
1[1] Un calcul manuel plus précis par une tierce personne donne (arrondi par défaut) 6.09 x 1015
2[2] Vopaliec, zine papier français consacré à Diplomatie et d’autres jeux, disponible auprès de la personne suivante : jeanpierremaulion-at-wanadoo.fr
3[3] Noter d’ailleurs au passage que les seuls conflits d’opposition possibles sur toute la carte sont entre ven et tri, et notre purge des oppositions avait donc soigneusement écarté ((Italie : ven – tri, rom t, nap t), (Autriche : tri – ven, vie t, bud t)).
4[4] Réalisation antérieure à la résolution de ce problème.
5[5] Noter le « ? » précédant les variables.
6[6] Conçu par C. Forgy en 1982.
7[7] Pour la compréhension des lecteurs non familiers d’UNIX, le signe « | » permet de rediriger la sortie d’un processus dans l’entrée d’un autre, et la commande « cat » liste le contenu d’un fichier.
DIPLOMANIA.FR: Un site qui a besoin de vous!
Nous avons besoin de vous pour develloper Diplomania.fr, un projet de site web Open Source permettant de jouer au jeu de société Diplomacy et d’échanger avec la communauté francophone du monde entier.
The Game That Ruins Friendships and Shapes Careers
For me, Diplomacy is an addictive quarantine hobby. For my high school frenemy, it was training for the Trump administration.
OCTOBER 23, 2020, 7:00 AM

In the absence of parties and happy hours and date nights, millions of Americans living under lockdown have regressed into pastimes like playing Animal Crossing, reading War and Peace, baking sourdough bread, or attempting to learn Romanian.
For me and around two dozen friends, the diversion of choice has been Diplomacy, the strategy board game invented by a Harvard University undergraduate named Allan B. Calhamer in the 1950s, mass-marketed by the game company Avalon Hill, and eventually developed into an elaborate (and mostly free) online hobby. My friends, some of whom had never played before the COVID-19 pandemic, have quickly become hopeless addicts. For me, Diplomacy has been an on-and-off obsession since high school, when I played it at the home of one Michael Ellis, then a young conservative, and now an obscure but potent player in the Trump administration. The lessons the game taught both of us stuck, but in very different ways.Trending Articles
If you’ve never played Diplomacy, it might be hard to explain its appeal. The game is not for everyone, but it is ideally suited for the kind of nerd who has a deep interest in international relations, geopolitics, or really politics of any kind—Foreign Policy’s readership, in other words. This is a game for people who dream about power in its purest form and how they might effectively wield it.
Beloved by President John F. Kennedy and former Secretary of State Henry Kissinger, Diplomacy models the realist view of international relations—in which sovereign states rationally compete for spheres of influence, eventually achieving a stable balance of power. The classic version of the game is set on a simplified map of Europe in 1901, at the height of the rivalry among the great imperial powers—England, France, Germany, Italy, Austria-Hungary, Russia, and Ottoman Turkey—that would eventually culminate in World War I. There are no dice, unlike in other classic strategy games like Risk or Axis & Allies, and there are only two types of game pieces: armies and fleets. Everything about Diplomacy is simple and easy to learn, but the actual gameplay is fiendishly complex, built around social interactions between seven committed players, each pursuing their own selfish interests through a series of ephemeral military pacts.From left: a classic Diplomacy board; a January 1974 cover of Games & Puzzles magazine featuring the creator of the strategy game, Allan B. Calhamer; and a version of the game designed by David Klion and Manoli Strecker set in a near-future post-apocalyptic New York City. COURTESY PHOTOS
Part of what keeps Diplomacy interesting is its versatility—there are dozens if not hundreds of variant maps spanning regions and eras. In recent months, my friends and I have played variants set in the Western Hemisphere of the 1840s and in a near-future post-apocalyptic New York City, and we are currently deep into a 21-player global-scale variant set in the aftermath of the Napoleonic Wars (we designed the last two of those ourselves). But the spirit of the game is rooted in that pre-World War I moment when the Western imperial powers coldly, amorally divided up the rest of the world between them while maneuvering for strategic advantage in Europe—a fun, gentlemanly board game for them and a series of massacres, genocides, and myriad other oppressions for millions of people on every continent who didn’t get to play. There are no moral or ideological distinctions among the great powers; aside from geographic circumstances, one plays the German kaiser, the British prime minister, or the Ottoman sultan exactly the same way. Diplomacy encourages its players to imagine themselves as grand negotiators redrawing borders with international peers at a summit, not as rulers charged with upholding any set of religious, national, or democratic values.
I bring all this up not to “cancel” Diplomacy, without which my quarantine would be a great deal more monotonous, but simply to note why it might be considered good preparation for being a political operative in Washington.
I bring all this up not to “cancel” Diplomacy, without which my quarantine would be a great deal more monotonous, but simply to note why it might be considered good preparation for being a political operative in Washington. As the name implies, most of the game is spent negotiating—forming secret alliances, divvying up proposed territorial gains, playing rival powers off one another, and spreading disinformation. Each player submits secret orders, which are then revealed and executed simultaneously, after which negotiations resume (repeat ad nauseam). There are no formal penalties for lying to another player, though one’s reputation may suffer, and the damage can outlast any one game. Diplomacy is famous for ending friendships; as a group activity, it requires opt-in from players who are comfortable casually manipulating one another. It’s certainly possible to possess such skills without deploying them in one’s career—as a freelance writer, my own manipulations extend only to guilting my editor when I see he’s playing online video games on Steam. But should one wish to enter the upper echelons of Beltway politics—the cynical world of This Town, the proverbial swamp that President Donald Trump pledged to drain and instead naturally adapted to—Diplomacy is an ideal training ground.
In a satisfying game of Diplomacy, where nobody flakes out because of other commitments, shifting great-power blocs will gradually whittle Europe down from seven powers to a more manageable four or three, who will then agree to a draw—or fail to do so, thus paving the way for a solo victory by the most ruthless player. Classic Diplomacy requires exactly seven players, no more and no less, and each must be willing to commit a large block of time to the game. In person, this might mean a chaotic afternoon at a house big enough for multiple players to pair off in separate rooms for scheming. The combination of a global pandemic and the internet makes setting this up much easier. There are free websites, such as PlayDiplomacy or Backstabbr, where strangers or groups of friends can arrange games to be played out over multiple weeks, with orders submitted every 12 or 24 hours and thus plenty of time for lengthy correspondences by email, phone, text, or direct message.
But if you’re a teenager, the time commitment needed for an in-person game is a lot more plausible. My own teenage Diplomacy frenzy took place two decades ago and almost exactly a century after the classic game is set. Our little clique, spread out among several D.C.-area high schools, would meet at Michael Ellis’s house in suburban Maryland and spend whole weekend afternoons plotting and backstabbing while totally sober. (We were very cool.) I’m still friends with a few members of that crowd, but not with our host, who in a narrow sense has gone on to greater success and influence than the rest of us—an achievement reached, perhaps, by fully internalizing Diplomacy’s cynical realpolitik.
David Klion

Global Diplomacy 1821 map created by David Klion and Manoli Strecker
Cartes prototypes Diplomaty des annees 1950 – Lot de la propriete Allan Calhamer

Trouvé sur le domaine d'Allan Calhamer ... Lot de 7 cartes / dessins / prototypes de jeu de diplomatie - Les deux cartes peintes sont sur papier kraft épais et une fois déroulées, mesurent 42 x 29,5 "(photo 1), 42 x 28" (photo 2) et les 5 cartes papier mesurent 11 x 8,5 "(photo 4) et plus. La carte de la photo 4 est sur papier calque et les notes en haut sont agrandis sur les photos 5 et 6, on pense qu'il s'agit de dessins ou de cartes prototypes originaux - nous n'en sommes pas sûrs à 100%, mais nous avons consulté l'expert en diplomatie Larry Peery avec des photos des deux cartes peintes qui à écrit à leur sujet dans le numéro actuel de "Diplomacy World" (numéro 137 du printemps 2017) ... , les cartes sont peintes à la détrempe. sur papier épais (presque certainement par Allan lui-même) à la fin des années 1950. Je crois qu'il s'agissait de prototypes originaux utilisés pour jouer au jeu de test avant qu'Allan n'imprime les 500 premiers exemplaires du jeu à la fin des années 1950. . Je n'ai vu le dos d'aucune des deux cartes, mais il ne fait aucun doute dans mon esprit qu'il s'agit d'originaux authentiques.
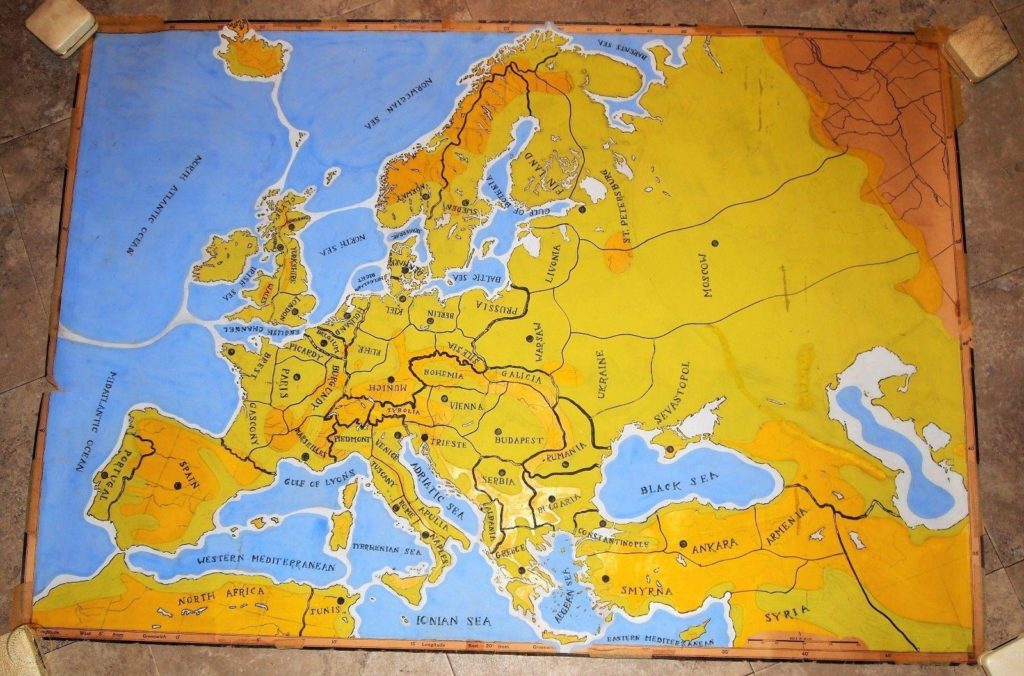
La carte du haut est à peu près la carte de diplomatie telle que nous le connaissons de l'édition Allan B.Calhamer ou de la première édition de Games Research. Je suppose que c'est l'archétype de diplomatie. comme le jeu que nous connaissons et aimons.

Encore plus intrigante pour moi est la deuxième carte; qui est à peu près la même taille, le même matériau... Je soupçonne que c'était une version antérieure de la carte finale. "" Comme vous pouvez le voir, il y a des différences majeures entre les deux. Ces différences ont été discutées par d'autres, comme Edi Birsan, et ont finalement abouti à une simplification de la carte plus jouable et équilibrée. Remarquez la différence dans la façon dont le milieu de l'océan Atlantique est traité. La France a une Bourgogne divisée en deux espaces, l'Allemagne a un autre espace à l'ouest, l'Autriche a un autre espace et la Turquie est très différente Je suis sûr que vous pouvez trouver d'autres différences. Une œuvre d'art peinte par Allan lui meme!
Championnat du Monde Francophone Results
Congratulations to Cyrille Sevin who won the tournament of 32 players with an 11-centre Austrian board top in the finals. A big thank you to French-Speaking World Championship organiser Nicolas Sahuguet. You can check out the games and final scores here.
To those who made the final board but fell short, we salute you and wish a speedy emotional recovery to Emmanuel duPontavice, Sacha Massicard, Ruben Sanchez, Christophe Borgeat, Candice Rocher and Olivier Prigent.
If you’d like to get to know this great community of French speaking Diplomacy players, visit their discord server.
CDFv
For your greatest pleasure, our Bouclette went to interview top board players to collect their post-match thoughts and analysis.La nouvelle carte de Diplomania par IDoBraaaa
oui, un test !!
Le draft de la carte de DIPLOMANIA – travail en cours en ce moment par IDoBraaaa.